在工作中最有用的一种分类法就是把人分为影响力高的和影响力低的。影响力在我的定义里面严格等于“让事情发生的能力” (The ability to make things happen)。
作为一个理科生,如果不能拿数学表达一个概念总觉的自己没想清楚。所以我做了如下的公式来分析影响力。
我们定义Y是事情发生的程度,或者可以也可以简单的定义为事情是否发生(1或者0)。 Y是很多因素的函数:
Y = 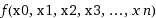
x0到xn分别代表要让事情成功的所有的因素。
x0定义为我们所关注的那个人的因素,其他的可以是任何影响成功的因素,比如x1定义为所在的公司,x2定义为他的经理,x3定义为他的团队,x4定义为宏观环境,x5定义为竞争对手,x100定义为天气,x101定义为是否有恐怖袭击等等。这个概念的表达式就是在表达一个事情的成功真的是由很多的因素决定的。
每个人做不成一件事情一定会列举x1到xn中间的某个原因。而我认为,当一件事情的成败和x0关系越大就说明这个人的影响力越大,跟x0以外的部分关系越大就说明这个人的影响力越小。
若是用线性表达式来非常粗略的表达函数 f( ) 的话,上述公式可以变形为:
Y = a0 * x0 + a1 * x1 + a2 * x2 + … + an * xn
a0 到 an 是指定的因素的重要度的因子。
我把一个人的影响力i0定义为:
i0 = a0 / ( a0 + a1 + a2 + … + an) * 100%
也就是说,此人对于成功的影响占所有因素的比例。比例越高,影响力越高,或者说让事情发生的能力就越大。
即便是一件事情不是由自己直接控制的,影响力强的人总有办法把x1到xn中间影响比较大的因素变成自己的一个函数,比如x1 = f'(x0)。若用线性表达,就是 x1 = b * x0。代入原来的公式,一个不稳定的因素消失了,a0变大了,从 a0 变成了 (a0 + b * a1)。
人的大脑其实都在做数据挖掘。当足够多的事情累积的时候,我们用最简单的线性回归对那么多事情进行分析,对于一个人的a0到底是多少还是心里有数的。你会发现就是有一群人,无论x1到xn对于结果有多少逆向的影响,他总能比较大概率的做成一件事情;而另外一些人,即使在外界都顺风顺水,看起来不存在什么大的可变因素的时候搞砸一件事情。
当一件事情做不成的时候,没必要去花太多的精力去埋怨x1到xn不配合,仅仅是因为自己的a0不够大而已。若是没有x1到xn这些因素的羁绊,我们还需要让事情发生的人x0来做什么呢?